灯塔（LightHouse）

描述

海上有许多灯塔，为过路船只照明。

（图一）

如图一所示，每个灯塔都配有一盏探照灯，照亮其东北、西南两个对顶的直角区域。探照灯的功率之大，足以覆盖任何距离。灯塔本身是如此之小，可以假定它们不会彼此遮挡。

（图二）

若灯塔A、B均在对方的照亮范围内，则称它们能够照亮彼此。比如在图二的实例中，蓝、红灯塔可照亮彼此，蓝、绿灯塔则不是，红、绿灯塔也不是。

现在，对于任何一组给定的灯塔，请计算出其中有多少对灯塔能够照亮彼此。

输入

共n+1行。

第1行为1个整数n，表示灯塔的总数。

第2到n+1行每行包含2个整数x, y，分别表示各灯塔的横、纵坐标。

输出

1个整数，表示可照亮彼此的灯塔对的数量。

样例

输入

3
2 2
4 3
5 1

输出

1

限制

对于90%的测例：

对于95%的测例：

全部测例：

灯塔的坐标x, y是整数，且不同灯塔的x, y坐标均互异

时间：2 sec

内存：256 MB

提示

注意机器中整型变量的范围，C/C++中的int类型通常被编译成32位整数，其范围为，不一定足够容纳本题的输出。

算法思路

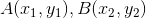
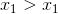
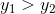
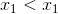
根据题意，对于灯塔对，只需且，或者且即可

解法一：暴力解法

struct Point
{
	int x = 0;
	int y = 0;
};

Point* points = new Point[4000001];

bool isGroup(Point& a, Point& b)
{
	return (a.x > b.x && a.y > b.y || a.x < b.x && a.y < b.y);
}

int main()
{

	int n = 0;
	scanf("%d\n", &n);

	for (int i = 0; i < n; ++i)
	{
		scanf("%d\n", &points[i].x);
		scanf("%d\n", &points[i].y);
	}

	int rel = 0;
	for (int i = 0; i < n - 1; ++i)
	{
		for (int j = i + 1; j < n; ++j)
		{
			if (isGroup(points[i], points[j]))
				rel++;
		}
	}

    printf("%d\n", rel);
}

解法二：

先将各个灯塔根据x坐标排序，然后取出y坐标，对y坐标进行归并排序的同时，计数“顺序对”，将B数组（下标为j，lo~mi）与C数组（下标为k，mi~hi）归并时，当B[j] < C[k]，B[j]也必小于C[k + mi]~C[hi]，构成(hi - mi - k)个顺序对

#include <cstdio>

struct Point
{
	int x = 0;
	int y = 0;
};
bool isGroup(Point& a, Point& b);
void merge(Point* points, int lo, int mi, int hi); 
void mergeSort(Point* points, int lo, int hi);
long long invInside(int* pointYs, int lo, int hi);
long long invBetween(int* pointYs, int lo, int mi, int hi);


Point* points = new Point[4000001];
Point* B = new Point[4000001];
int*  pointYs = new int[4000001];
int* BY = new int[4000001];

int main()
{
#ifndef _OJ_
	freopen("input.txt", "r", stdin);
	freopen("output.txt", "w", stdout);
#endif
	//setvbuf(stdin, new char[1 << 20], _IOFBF, 1 << 20);

	int n = 0;
	scanf("%d\n", &n);

	for (int i = 0; i < n; ++i)
	{
		scanf("%d\n", &points[i].x);
		scanf("%d\n", &points[i].y);
	}
	mergeSort(points, 0, n);
	for (int i = 0; i < n; ++i)
		pointYs[i] = points[i].y;
	long long rel = invInside(pointYs, 0, n);
	printf("%lld\n", rel);

#ifndef _OJ_
	fclose(stdin);
	fclose(stdout);
#endif
	return 0;
}

bool isGroup(Point& a, Point& b)
{
	return (a.x > b.x && a.y > b.y || a.x < b.x && a.y < b.y);
}

void merge(Point* points, int lo, int mi, int hi)
{
	Point* A = points + lo;
	int lb = mi - lo; // Point* B = new Point[lb];
	for (size_t i = 0; i < lb; B[i] = A[i++]);
	int lc = hi - mi; Point* C = points + mi;

	for (int i = 0, j = 0, k = 0; j < lb; )
	{
		if (lc <= k || B[j].x < C[k].x) A[i++] = B[j++];
		if (k < lc && C[k].x <= B[j].x) A[i++] = C[k++];
	}
	//delete[] B;
}

void mergeSort(Point* points, int lo, int hi)
{
	if(hi - lo < 2) return;
	int mi = (hi + lo) >> 1;
	mergeSort(points, lo, mi);
	mergeSort(points, mi, hi);
	merge(points, lo, mi, hi);
}

long long invInside(int* pointYs, int lo, int hi)
{
	long long rel = 0;
	if (hi - lo < 2) return 0;
	const int mi = (lo + hi) >> 1;
	rel += invInside(pointYs, lo, mi);
	rel += invInside(pointYs, mi, hi);
	rel += invBetween(pointYs, lo, mi, hi);
	return rel;
}
long long invBetween(int* pointYs, int lo, int mi, int hi)
{
	int* A = pointYs + lo;
	int lb = mi - lo; // int* B = new int[lb];
	for (size_t i = 0; i < lb; BY[i] = A[i++]);
	int lc = hi - mi; int* C = pointYs + mi;
	long long num = 0;
	for (size_t i= 0, j = 0, k = 0; j < lb;)
	{
		if (lc <= k || (BY[j] <= C[k]))
		{
			A[i++] = BY[j++];
			if (k < lc)
				num += lc - k;
		}
		if ((k < lc) && C[k] <= BY[j])
			A[i++] = C[k++];
	}
	//delete[] B;
	return num;
}

不预先定义归并排序Point数组B，与Y坐标数组归并排序的数组B，会超时 

转载自原文链接, 如需删除请联系管理员。

原文链接：灯塔（LightHouse），转载请注明来源！