一、香农编码
概念：
香农编码是是采用信源符号的累计概率分布函数来分配字码的。香农编码是根据香农第一定理直接得出的，指出了平均码长与信息之间的关系，同时也指出了可以通过编码使平均码长达到极限值。香农第一定理是将原始信源符号转化为新的码符号，使码符号尽量服从等概分布，从而每个码符号所携带的信息量达到最大，进而可以用尽量少的码符号传输信源信息。
香农编码属于不等长编码，通常将经常出现的消息变成短码，不经常出现的消息编成长码，从而提高通信效率。 香农编码严格意义上来说不是最佳码，它是采用信源符号的累计概率分布函数来分配码字。
编码步骤如下：
(1)将信源符号按概率从大到小顺序排列，为方便起见，令
；
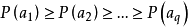(2)按
计算第i个符号对应的码字的码长(取整)；
(3) 计算第i个符号的累加概率 ；
(4)将累加概率变换成二进制小数，取小数点后 位数作为第i个符号的码字。
香农编码的效率不高，实用性不大，但对其他编码方法有很好的理论指导意义。一般情况下，按照香农编码方法编出来的码，其平均码长不是最短的。即不是紧致码(最佳码)。只有当信源符号的概率分布使不等式左边的等号成立时，编码效率才达到最高
例1对如下信源编码：
其香农编码如表所示，
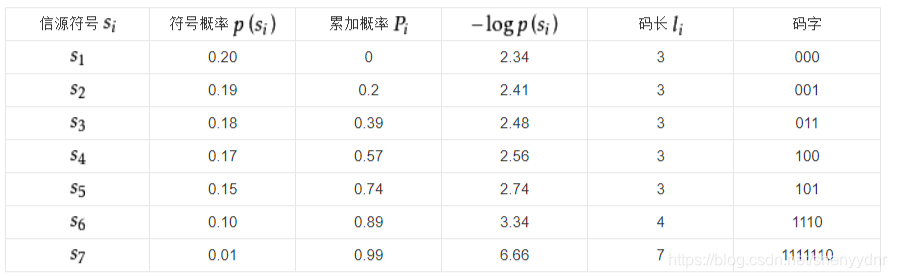
以i=4为例，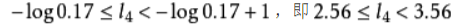
因此
。累加概率 ，变成二进制数，为0.1001…。转换的方法为：用Pi乘以2，如果整数部分有进位，则小数点后第一位为1，否则为0，将其小数部分再做同样的处理，得到小数点后的第二位，依此类推，直到得到了满足要求的位数，或者没有小数部分了为止。可以看出，编码所得的码字，没有相同的，所以是非奇异码，也没有一个码字是其他码字的前缀，所以是即时码，也是唯一可译码。
平均码长为：(0.2+0.19+0.18+0.17+0.15)x3+0.1x4+0.01x7=3.14
特点：
香农编码的效率不高，实用性不大，但对其他编码方法有很好的理论指导意义。一般情况下，按照香农编码方法编出来的码，其平均码长不是最短的，即不是紧致码(最佳码)。只有当信源符号的概率分布使不等式左边的等号成立时，编码效率才达到最高。
**
二、哈夫曼编码
**
概念：
哈夫曼编码(Huffman Coding)，又称霍夫曼编码，是一种编码方式，哈夫曼编码是可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法，该方法完全依据字符出现概率来构造异字头的平均长度最短的码字，有时称之为最佳编码，一般就叫做Huffman编码（有时也称为霍夫曼编码）。
哈夫曼编码的具体步骤如下：
1）将信源符号的概率按减小的顺序排队。
2）把两个最小的概率相加，并继续这一步骤，始终将较高的概率分支放在右边，直到 最后变成概率１。
3）画出由概率１处到每个信源符号的路径，顺序记下沿路径的０和１，所得就是该符号的霍夫曼码字。
4）将每对组合的左边一个指定为0，右边一个指定为1（或相反）。
例1对如下信源编码：
通过以上步骤得到的编码为：
平均码长：0.2x2+0.19x2+0.18x3+0.17x3+0.15x3+0.1x4+0.01x4 = 2.72
特点
Huffman码具有以下3个特点：
- Huffman码的编码方法保证了概率大的符号对应短码，概率小的符号对应长码，而且短码得到充分利用。
- 每次缩减信源的最后两个码字总是最后一位码元不同，前面各位码元相同(二元编码情况)。
- 每次缩减信源的最长两个码字有相同的码长。
这三个特点保证了所得的Huffman码一定是最佳码。
三、费诺编码
概念：
1949年费诺(R.M. Fano)提出了一种编码方法，称之为费诺码或Fano码。它属于概率匹配编码，但一般也不是最佳的编码方法，只有当信源的概率分布呈现 分布形式的条件下，才能达到最佳码的性能 。
Fano码的编码步骤如下：
1)将 r 个信源符号按概率递减的方式进行排列 。
2)将排列好的信源符号按概率值划分成两大组，使每组的概率之和接近于相等，并对每组各赋予一个二元码符号0和1。
3)将每一大组的信源符号再分成两组，使划分后的两个组的概率之和接近于相等，再分别赋予一个二元码符号0和1。
4)依次下去，直至每个小组只剩一个信源符号为止。
5)将逐次分组过程中得到的码元排列起来就是各信源符号的编码。
例1对如下信源编码：
从左到右，所有的符号以它们出现的概率（次数）划分。在S3与S4之间划定分割线，得到了左右两组，总频率分别为0.57,0.43。
这样就把两组的差别降到最小。通过这样的分割, S1,S2与S3同时拥有了一个以0为开头的码字, S4,S5,S6,S7的码子则为1, 随后, 在树的左半边，于S1,S2,S3间建立新的分割线，S1为一组，S2，S3为一组这样S1就成为了码字为00的叶子节点，S2，S3的开头为01；然后S2,S3间再分组得到S2的编码为010,S3的编码为011.以此类推最后得到编码为下图：
**平均码长为：0.2x2+0.19x3+0.18x3+0.17x2+0.15x3+0.1x4+0.01x4= 2.74
Fano码具有以下性质：
1)Fano码的编码方法实际上是一种构造码树的方法，所以Fano码是即时码。
2)Fano码考虑了信源的统计特性，使概率大的信源符号能对应码长较短的码字，从而有效地提高了编码效率。
3)Fano码不一定是最佳码。因为Fano编码方法不一定能使短码得到充分利用。当信源符号较多时，若有一些符号概率分布很接近，分两大组的组合方法就会很多。可能某种分大组的结果，会使后面小组的“概率和”相差较远，从而使平均码长增加。
前面讨论的Fano码是二元Fano码，对于s元Fano码，与二元Fano码的编码方法相同，只是每次分组时应将符号分成概率分布接近的s个组。
转载自原文链接, 如需删除请联系管理员。
原文链接：香农编码，哈夫曼编码与费诺编码的比较，转载请注明来源！