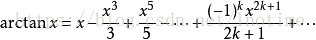1. 公式准备
计算准确圆周率的马青公式:
对反正切进行级数展开:
就可以得到
π = 16(1/5 - 1/3/5^3 + 1/5/5^5 - ...) - 4(1/239 - 1/3/239^3 + 1/5/239^5 - ...)
π = (16/5 - 4/239) + (- 16/5^3/3 + 4/239^3/3) + (16/5^5/5 - 4/239^5/5) + ...

2. 用 Python 实现
π 的公式已经拿到,我们有一个明确的想要精确的π的位数,那么当式子中n越大的时候,第n项就会越小,小到计算这个精确目标时可以忽略的地步。
注意1:由于程序中浮点数的有效位数有限(小数点后很长的话会被省略,很大的数如果是小数也会用科学技术法),会损失很大精度,所以用整数来计算π。
比如想计算小数点后 7 位,就计算 π * 10^7 是多少,返回 31415926。
比如想计算小数点后 3 位,程序就会给你返回整数 3141,是扩大了 10^3 的结果。
注意2: 想用整数计算 π,那除法的时候就要使用取模运算来保证结果也是整数,以达到保证精度的目的。
注意3: 我用取模操作代替了除法,但是取模对于除法来说本身就是有精度损失的,为了弥补这部分精度,我采取的方案是,先把想精确的位数增加 k,最后把结果减少 k 位。
注意4: 从这句话以后的 n,不再指代上面求 π 的数学公式中的 n,而代表输入的想要精确 π 的位数。
可以预见,注意3中提出的这个方案是有漏洞的,因为 k 是被固定在程序中的,随着用户输入 n 的增大,越来越大量的取模运算损失的精度,必定是固定不变的 k 值所不能弥补的。所以对每一个固定的 k,一定会有一个 n 值,使得本程序所计算的结果是错误的。
对此,我还有一个方案,k 值不固定,由 n 计算得出,n 越大就取越大的 k。但我不想随便定一个 k 与 n 的关系,当然通过代码可以试出一个不错的,但程序计算总有尽头,没有理论支持就无法证明这个关系是真正合理的。
def pi(n):
p = 10 ** (n + 10) # 准备初始整数,先多乘 k 个 0,以增加精度,最后再去掉,这里我取 k=10
a = p * 16 // 5 # 第一项的前半部分
b = p * 4 // -239 # 第一项的后半部分
f = a + b # 第一项的值
p = f # π
j = 3
while abs(f): # 当|f|=0后计算π的值就不会再改变了
a //= -25 # 第n项的前半部分
b //= -57121 # 第n项的后半部分
f = (a + b) // j
p += f
j += 2
return p // 10**10 # 去掉 k 位,k=10我还专门写了验证程序来验证取不同 k 时到底 n 为多大计算结果开始不准确。
经过验证,当 k 分别取 1 到 9 时,输入 n 的值为 8, 31, 158, 306, 359, 4254, 13389, 17533, 17533 (对,8和9是一样的)时,计算结果开始出现误差。当 k 取 10 时,n 取 100000 还都没有出现误差。
转载自原文链接, 如需删除请联系管理员。
原文链接:【Python、数学】计算任意位数的圆周率π(马青公式),转载请注明来源!