首页 » 技术分享 » 二分图

二分图

　
评论关闭　928次浏览

先放三个链接：
将概念讲的很清晰：http://www.renfei.org/blog/bipartite-matching.html
将代码写的很清晰： http://blog.csdn.net/c20180630/article/details/70175814
相关题目：http://blog.csdn.net/acmman/article/details/38421239

概念：

这篇文章讲无权二分图（unweighted bipartite graph）的最大匹配（maximum matching）和完美匹配（perfect matching），以及用于求解匹配的匈牙利算法（Hungarian Algorithm）；不讲带权二分图的最佳匹配。

二分图

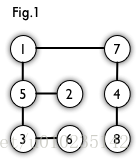
简单来说，如果图中点可以被分为两组，并且使得所有边都跨越组的边界，则这就是一个二分图。准确地说：把一个图的顶点划分为两个不相交集 U 和V ，使得每一条边都分别连接U、V中的顶点。如果存在这样的划分，则此图为一个二分图。二分图的一个等价定义是：不含有「含奇数条边的环」的图。图 1 是一个二分图。为了清晰，我们以后都把它画成图 2 的形式。

匹配：

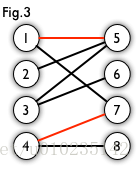
在图论中，一个「匹配」（matching）是一个边的集合，其中任意两条边都没有公共顶点。例如，图 3、图 4 中红色的边就是图 2 的匹配。
这里写图片描述这里写图片描述这里写图片描述这里写图片描述

我们定义匹配点、匹配边、未匹配点、非匹配边，它们的含义非常显然。例如图 3 中 1、4、5、7 为匹配点，其他顶点为未匹配点；1-5、4-7为匹配边，其他边为非匹配边。

最大匹配：

一个图所有匹配中，所含匹配边数最多的匹配，称为这个图的最大匹配。图 4 是一个最大匹配，它包含 4 条匹配边。

完美匹配：

如果一个图的某个匹配中，所有的顶点都是匹配点，那么它就是一个完美匹配。图 4 是一个完美匹配。显然，完美匹配一定是最大匹配（完美匹配的任何一个点都已经匹配，添加一条新的匹配边一定会与已有的匹配边冲突）。但并非每个图都存在完美匹配。

举例来说：如下图所示，如果在某一对男孩和女孩之间存在相连的边，就意味着他们彼此喜欢。是否可能让所有男孩和女孩两两配对，使得每对儿都互相喜欢呢？图论中，这就是完美匹配问题。如果换一个说法：最多有多少互相喜欢的男孩/女孩可以配对儿？这就是最大匹配问题。
这里写图片描述

求解最大匹配问题的一个算法是匈牙利算法，下面讲的概念都为这个算法服务。
这里写图片描述

交替路：从一个未匹配点出发，依次经过非匹配边、匹配边、非匹配边…形成的路径叫交替路。

增广路：从一个未匹配点出发，走交替路，如果途径另一个未匹配点（出发的点不算），则这条交替路称为增广路（agumenting path）。例如，图 5 中的一条增广路如图 6 所示（图中的匹配点均用红色标出）：
这里写图片描述

增广路有一个重要特点：非匹配边比匹配边多一条。因此，研究增广路的意义是改进匹配。只要把增广路中的匹配边和非匹配边的身份交换即可。由于中间的匹配节点不存在其他相连的匹配边，所以这样做不会破坏匹配的性质。交换后，图中的匹配边数目比原来多了 1 条。

我们可以通过不停地找增广路来增加匹配中的匹配边和匹配点。找不到增广路时，达到最大匹配（这是增广路定理）。匈牙利算法正是这么做的。

匈牙利算法

用增广路求最大匹配(称作匈牙利算法，匈牙利数学家Edmonds于1965年提出)

算法轮廓：

置M为空
找出一条增广路径P，通过取反操作获得更大的匹配M’代替M
重复2操作直到找不出增广路径为止

找增广路径的算法

我们采用DFS的办法找一条增广路径：
从X部一个未匹配的顶点u开始，找一个未访问的邻接点v（v一定是Y部顶点）。对于v，分两种情况：

1、如果v未匹配，则已经找到一条增广路
2、如果v已经匹配，则取出v的匹配顶点w(w一定是X部顶点)，边(w,v)目前是匹配的，根据“取反”的想法，要将(w,v)改为未匹配，(u,v)设为匹配，能实现这一点的条件是看从w为起点能否新找到一条增广路径P’。如果行，则u-v-P’就是一条以u为起点的增广路径。

代码：

//伪代码
bool dfs(int u)//寻找从u出发的增广路径
{
    for each v∈u的邻接点
        if(v未访问){
            标记v已访问;
            if(v未匹配||dfs(cy[v])){
                cx[u]=v;
                cy[v]=u; 
                return true;//有从u出发的增广路径
            }
        }
    return false;//无法找到从u出发的增广路径
}
//代码
bool dfs(int u){
    for(int v=1;v<=m;v++)
        if(t[u][v]&&!vis[v]){
            vis[v]=1;
            if(cy[v]==-1||dfs(cy[v])){
                cx[u]=v;cy[v]=u;
                return 1;
            }
        }
    return 0;
}
void maxmatch()//匈牙利算法主函数
{
    int ans=0;
    memset(cx,0xff,sizeof cx);
    memset(cy,0xff,sizeof cy);
    for(int i=0;i<=nx;i++) 
        if(cx[i]==-1)//如果i未匹配
        { 
            memset(visit,false,sizeof(visit)) ; 
            ans += dfs(i); 
        }
    return ans ;
}

算法分析

算法的核心是找增广路径的过程DFS
对于每个可以与u匹配的顶点v，假如它未被匹配，可以直接用v与u匹配；
如果v已与顶点w匹配，那么只需调用dfs(w)来求证w是否可以与其它顶点匹配，如果dfs(w)返回true的话，仍可以使v与u匹配；如果dfs(w)返回false,则检查u的下一个邻接点…….
在dfs时，要标记访问过的顶点（visit[j]=true），以防死循环和重复计算；每次在主过程中开始一次dfs前，所有的顶点都是未标记的。
主过程只需对每个X部的顶点调用dfs，如果返回一次true，就对最大匹配数加一；一个简单的循环就求出了最大匹配的数目。

相关题目：

http://blog.csdn.net/acmman/article/details/38421239

我的代码：
//Erfentu.h

#ifndef __ERFENTU_H
#define __ERFENTU_H
#define MAXNUMER 512

bool dfsER(int i);

int initialAndFind();

#endif

//Erfentu.cc

#include "erfentu.h"
#include <string.h>

int verx[MAXNUMER][MAXNUMER];
int cau[MAXNUMER];
int cav[MAXNUMER];
bool visited[MAXNUMER];

int nowmaxU;
int nowmaxV;

bool dfsER(int u)
{
    for (int v = 1; v <= nowmaxV; ++v)
    {
        if (verx[u][v] != -1 && !visited[v])
        {
            visited[v] = true;
            if (cav[v] == -1 || dfsER(cav[v]))
            {
                cau[u] = v;
                cav[v] = u;
                return true;
            }
        }
    }
    return false;
}

int initialAndFind()
{

    memset(cau, -1, MAXNUMER*sizeof(int));
    memset(cav, -1, MAXNUMER*sizeof(int));
    int ans = 0;
    for (int i = 1; i <= nowmaxU; ++i)
    {
        memset(visited, false, MAXNUMER);
        if (dfsER(i))
            ++ans;

    }
    return ans;
}

//main.cc


#include "erfentu.h"

#include <stdlib.h>
#include <iostream>
using namespace std;

extern int verx[MAXNUMER][MAXNUMER];
extern int cau[MAXNUMER];
extern int cav[MAXNUMER];
extern bool visited[MAXNUMER];

extern int nowmaxU;
extern int nowmaxV;


int main()
{
```memset(verx, -1, MAXNUMER*MAXNUMER*sizeof(int));
    int K, M, N;
    cin >> K >> M >> N;
    nowmaxU = M;
    nowmaxV = N;
    int x, y;
    while (K > 0)
    {
        cin >> x >> y;
        verx[x][y] = 1;
        K--;
    }
    cout << initialAndFind() << endl;
    system("pause");
    return 0;
}

转载自原文链接, 如需删除请联系管理员。

原文链接：二分图，转载请注明来源！

赞 0