| SPSS |  |
| 变量尺度跟数据类型 |  |
| 百分位值:将数据从小到大排序,用n-1个数据点将数据分成n等份 |  |
| 集中趋势:反映数据向其中心值凝聚的程度,对数据一般水平的概括性度量 |  |
| 离散趋势:反映数据偏离中心值的程度,是衡量集中趋势值对整个数据的代表程度。数据离散程度越大,集中趋势值代表性越低;反之,离散程度越接近于0,集中趋势值代表性越高 |  |
| 条形图和直方图差别 |
|
| 描述分析与频率分析差异 |
|
| 交叉表分析 |
|
| 多选题 |
多重响应集(二分类和多重分类法)
|
| 报表类型 |
1、叠加表:是指同一张表中有多个同类变量的描述分析结果 2、交叉表:是一种行列交叉的分类汇总表格,行和列上至少各有一个分类变量,行和列的交叉处可对数据进行多种汇总计算 3、嵌套表:是指多个变量放置在同一个表格维度中,分析维度是由两个及以上变量的各种类别组合而成。在展现较多统计指标时,使结果更为美观和紧凑 |
| 最小二乘法:最小平方法 |
|
调整后 关系(判定系数、决定系数、拟合优度) 关系(判定系数、决定系数、拟合优度) |
|
| 回归系数的显著性检验 | 研究回归模型中的每个自变量与因变量之间是否存在显著的线性关系,即研究自变量能否有效地解释因变量的线性变化,它们能否保留在线性回归模型中 |
| 标准化回归系数 |
用来测量自变量对因变量的重要性,只有将因变量和自变量标准化到统一的量纲下才能进行重要性的比较与衡量。 若进行模型的使用与预测,需要使用非标准化系数。 |
|
回归线性自变量方法 输入:简单线性回归 步进(逐步):多重 |
 |
| 自动线性建模 |
定义:是在经常使用的一般线性模型基础上加以改进,让用户输入最少的参数而自动线性建模的一个功能。 特点:连续变量、分类变量均可作为自变量参与建模 能自动寻找对因变量重要性最大的自变量,舍弃重要性很小或不重要的自变量,可以不用关心 如何选择自变量,自动化的过程会根据数据的特征选择最佳的自变量 还会自动进行离群值和缺失值处理,并输出一系列图表来展示回归模型的效果及相关信息 |
| 模型变量筛选 |
|
| 信息条件/信息准则 |
|
| Logistic回归 |
|
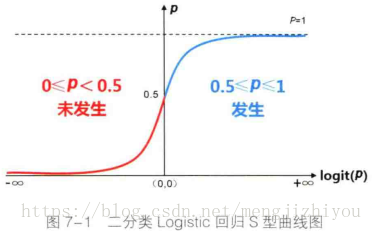
| 因变量跟概率值P的关系 |
|
| Logistic回归与线性回归的区别 |  |
| Logistic回归应用场景 |  |
| 时间序列分析 |
1、定义:是按时间顺序排列的一组数据序列。时间序列分析就是发现这组数据的变动规律并用于预测的统计技术 2、基本特点:假设事物发展趋势会延伸到未来 预测所依据的数据具有不规则性 不考虑事物发展之间的因果关系 3、时间序列的四种因素 4、四种因素组合方式
5、乘法加法模型分判断:根据序列图趋势判别
|
|
因素分解原因
|
|
| 四种因素的分解 |
1、通常情况下,会考虑季节因素的分解,将季节变动因素从原时间序列中去除,并生成由剩余的三种因素构成的序列来满足后续分析需求 2、只分解季节因素:因为时间序列中的长期趋势反映了事物发展规律,是研究的重点;循环变动由于周期较长,可近似看作是长期趋势的反映;不规则变动由于不容易测量,通常不单独分析;但季节变动的存在有时会让预测模型误判其为不规则变动,降低模型的预测精度。所以,当一个时间序列具有季节变动特征时,在预测之前会先将其季节因素进行分解 3、
|
| 时间序列步骤 |
|
| 平稳性 |
1、是指时间序列的所有统计性质都不会随着时间的推移而发生变化,对一个平稳的时间序列来说,具有以下特征: 均数和方差不随时间变化 自相关系数只与时间间隔有关,与所处的时间无关 2、自相关系数:相关系数是用来量化变量之间的相关程度的,自相关系数研究的是一个序列中不同时期的相关系数,即时间序列计算其当前期和不同滞后期的一系列相关系数。 3、进行时间序列平稳化原因:目前主流时间序列预测方法都是针对平稳的时间序列进行分析的,但在实际中遇到的都是不平稳的,在分析时,需要首先识别序列的平稳性,且把不平稳的序列转换为平稳序列。一个时间序列只有被平稳化处理过,才能被控制和预测。 4、时间序列平稳化方法之一:差分
|
| ARIMA |
1、时间序列分析中常用的模型,全称为求和自回归移动平均模型(Auto Regression Integrated Moving Average) 2、模型为:
|
| 探索性分析:没有所谓的标准流程和答案,不同数据有不同的适用方法,即使相同的数据,应用不同的方法也可能得到不同的结果,只要能有效解决实际业务问题即可。 |
主要是运用一些分析方法从大量的数据中发现未知且有价值信息的过程。初步探索性分析,数据可视化是比较好的方法,然后试用统计分析方法深入发现数据背后信息。 方法:RFM分析、聚类分析、因子分析、对应分析 |
| RFM分析:就是根据客户活跃程度和交易金额贡献,进行客户价值细分的一种方法 |
1、组成
2、分析原理
3、分析过程 4、RFM分析接受分数据格式:
为了保证数据的精确性,建议采用交易数据格式分析。交易数据可以整理为客户数据,而客户数据无法还原为交易数据。从使用的自由程度来看,采用交易数据格式要优于客户数据格式。 5、分析结果变量解释 6、重点营销对象判断
|
| 聚类分析 |
1、定义:就是按照个体的特征将它们分类,目的在于让同一个类别内的个体之间具有较高的相似度,而不同类别之间具有较大的差异性。研究人员就能够根据不同类别的特征有的放矢地分析,并制定出适合用于不同类别的解决方案 2、聚类分析如何将个体划分为不同的类别:为了合理地进行聚类,需要采用适当的指标来衡量研究对象之间的联系紧密程度,常用指标“距离”和“相似系数(一般指相关系数)”。假设将研究对象采用点表示,聚类分析时,将距离较小的点或相似系数较大的点归为同一类,将距离较大的点或相似系数较小的点归为不同的类。 3、特点(特别之处):
4、应用场景
5、步骤
6、数据标准化原因:因为有时各个变量间的变量值的数量级别差异较大或者单位不一致,例如一个变量的单位是元,另一个变量的单位是百分比,数量级别差异较大,而且单位也不一致,无法直接进行 行比较或者计算距离和相似系数等指标。只有通过标准化处理,消除变量间量纲关系的影响,在同一标准下才能够进行比较或者计算距离和相似系数等指标。 7、聚类方法
不同之处:
8、二阶聚类分析:一种智能聚类分析方法,智能体现
质心:反映数据分布的平均位置,理解为连续变量的集中趋势,常用平均值表示。 9、聚类方法对比 |
| 因子分析:找出隐藏在变量背后具有共性的因子 |
1、定义:通过研究变量间的相关系数矩阵,把这些变量间错综复杂的关系归结成少数几个综合因子,并据此对变量进行分类的一种统计分析方法。由于归结出的因子个数少于原始变量个数,但是它们又包含原始变量的信息,故这一分析过程也称为降维。 2、目的:探索结构:在变量之间存在高度相关性时希望用较少的因子来概括其信息 简化数据:把原始变量转化为因子得分后,使用因子得分进行其他分析,比如聚类分析、回 归分析等 综合评价:通过每个因子得分计算出综合得分,对分析对象进行综合评价 3、基本思想:通过因子分析,原始变量会转变为新的因子,这些因子之间相关性较低,而因子内部的变量相关程度较高 4、基本概念:
5、分析步骤: 6、如何判断数据是否适合因子分析
7、旋转方法常用:最大方差法,该方法能使每个变量尽可能在一个因子上有较高的载荷,在其余的因子上载荷较小,方便对因子进行解释。 累积方差贡献率达到60%及以上,则说明因子对变量的解释能力尚可接受,达到80%及以上,说明因子对变量的解释能力非常好。 判断最佳因子数:通常选取曲线中较陡的位置所对应的因子个数(特征值-因子个数图)。 8、提取因子个数的标准: 9、综合得分:贡献方差占比 |
| 对应分析:能够把一个交叉表结果通过图形的方式展现出来,用以表达不同变量之间以及不同类别之间的关系(交叉表图形化) |
1、对应分析可对数据进行降维处理,不过变量都是分类变量 2、定义:对应分析是一种多元统计分析技术,主要用于研究分类变量构成的交叉表,以揭示变量间的关系,并将交叉表的信息以图形的方式展示出来。主要适用于有多个类别的分类变量,可揭示同一个变量各个类别之间的差异,以及不同变量各个类别之间的对应关系。 3、对应分析看似是一种作图的技术,实际上难点在于对变量的选择。有些变量被忽视掉后,分析结果可以偏概全,没有揭示变量间真正的关系。通常情况下,可通过尝试不同变量的组合,以发现具有价值的信息。 4、以图形方式表达分类变量之间关系,优势: 5、劣势
6、实际工作中应用:主要应用于产品定位、品牌研究、市场细分、竞争分析、广告研究等领域,因为它是一种图形化的数据分析方法,能够将几组看似没有联系的数据,通过视觉上可以接受的定位图展现出来。 7、对应分析的操作关键主要是两点:
8、对比分析图
|
转载自原文链接, 如需删除请联系管理员。
原文链接:谁说菜鸟不会数据分析(SPSS篇)----- 学习笔记,转载请注明来源!