回忆上一节，对如下的原问题：
（1）
我们定义了拉格朗日对偶函数：
然后我们证明了：，其中p*是原问题的最优值。
也就是说我们找到了原问题最优值的一个下界。既然我们找到了一个下界，显然我们要找到它最好的下界。什么是最好的下界的？显然就是所有下界当中最大的那一个。所以我们要把
最大化，当然我们还要记得我们需要限制。我们把要优化的函数和约束条件正式写下来就是：
（2）
与原问题（1）相对应，我们把上面的问题（2）称作拉格朗日对偶问题（Lagrange dual problem）。显然，对偶问题的最优值d*就是我们可以获得的p*的最优下界，也就是所有下界中离p*最近的一个，它们的关系是：
（3）
我们把这个不等式叫做弱对偶性质（Weak Duality）。
顺其自然，我们可以引出一个重要的概念，对偶间隙，其定义为，用文字叙述就是原问题的最优值与通过拉个郎日对偶函数获得的其最好（最大）的下界之差。由不等式（3）可以看出，对偶间隙肯定是大于等于0的。
那么有没有可能在某种情况下，对偶间隙消失了呢？也就是说对偶问题的最优值与原问题的最优值相等了呢？
我们将要叙述一下Slater条件：
Slater条件：
存在x满足：
Slater条件即是说存在x，使不等式约束中的“小于等于号”要严格取到“小于号”。
可以证明，对于凸优化问题（关于凸优化问题，请参考维基百科），如果Slater条件满足了，则：
这种情况称为强对偶性质（Strong Duality）。
下面的问题是，如果对偶间隙消失了，会发生什么有趣的现象呢？
如果对偶间隙消失了，也就是说，如果对偶问题存在着最优点λ*,μ*并且使其对应的最优值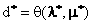
等于p*，这时会发生什么情况呢？还记得上一节我们证明的过程么：
（4）
在对偶间隙消失的情况下，中间所有的不等号都要变成等号：
（5）
注意，（5）中的λ和μ都加了星号，表示它们是对偶问题的最优点。（5）中有两个重要的等号，已经加了标记。
我们能得出什么结论？
1 .我们先来看等号1：
它说明了原问题的最优点x*是使取得最小值的点。
2. 我们再来看等号2：
它说明了：
由于我们限制了每一个λi≥0，所以上式中每一项都是非正的。这样我们又可以得出结论：
(6)
等式（6）被称作是互补性条件，我们可以把它换种写法：
或者写成它的等价形式（逆否命题）：
也就是说，只要一个不为0，另一个就必为0！
互补性条件有着重要的意义。它说明了当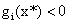
时，x*是处于可行域的内部的，这时不等式约束并不起作用，此时
；而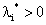
的点肯定是可行域边界的点（）。也就是说只有积极约束才有不为0的对偶变量。而这在支持向量机中有着重要的意义。回想在第一节我们最后的结论，支持向量机寻找最大间隔超平面可以归结为一个优化问题：
目标函数：
限制：
那么哪些不等式约束对应着不为0的对偶变量呢？显然，只有当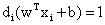
时，这个约束对应的对偶变量才可能不为0，而意味着什么？意味着这个约束对应的样本点xi是支持向量！也就是说：
只有支持向量才对应不为0的拉格朗日乘子！
转载自原文链接, 如需删除请联系管理员。
原文链接：支持向量机入门系列-4：对偶问题，转载请注明来源！