本文在抄自李世春老师博文叙述,学习参考。
1958年,程开甲院士在《物理学报》发表了题目为“用Fermi-Thomas 方法计算金属的结合能”[1]的文章,这是程先生发表的第一篇关于TFD模型的论文。此后,程先生就去搞×××研究,“他们终于第一次采取合理的TFD模型,计算出了×××爆炸时弹心的压力和温度”[2]。
25年后,程开甲院士和他的合作者发表了一系列关于TFD模型的论文,主要有:1984年在《物理学报》发表了“TF(或TFD)模型中原子的边界势及状态方程”[3];1991年在《力学进展》发表了“冷压状态方程计算的新方法和材料相图研究”[4];1993年在《自然科学进展》发表了“TFD模型和余氏理论对材料设计的应用”[5],在该论文中,程先生提出了“改进的TFD模型”,学术界称为TFDC模型或者程氏理论;1996年在《自然科学进展》(英文版)发表了TheoreticalFoundations of Condensed Materials[6],在该论文中,程先生第一次发表了元素周期表中38个元素的电子密度数据,即TFDC电子密度。程先生一直在坚持TFDC电子理论模型的研究,2005年还在《自然科学进展》发表研究论文[7]。
我于1993年开始接触到TFDC模型,并且认定“原子半径、TFDC电子密度和原子界面电子密度连续性条件”是TFDC模型的核心内容[8-10],TFDC电子密度是TFDC模型能够应用于其他理论的衔接点。10多年来,我查阅了3000多篇关于电子密度概念及其相关理论的文献资料,同时从理论和实验两方面对TFDC模型进行思考,现在把多年思考的主要结果归纳如下:
① 电子密度概念及其发展
电子密度ρ(x,y,z)是现代电子理论(如密度泛函理论,即DFT)中最核心的物理概念,被广泛应用在物理学、化学、材料科学和生物学等领域,成为现代科学应用最广泛的物理概念,显示出越来越重要的作用。电子密度的基本测量手段是X射线衍射(包括中子衍射),电子密度的理论计算方法是量子力学(1926年建立量子力学的波动方程)。1915年,Debye在关于X射线衍射的文章中提出了电子在原子中的分布问题,而且还强调了X射线衍射是探测原子中电子分布的基本方法[11]。1917年,Compton在关于X射线衍射的文章中明确提出了电子密度的概念[12]。
经典的TFD方法是密度泛函理论(DFT)思想的起源,也是现代DFT理论的一种最简单的近似方法。Bader建立的Atomsin Molecules(AIM)理论[13-14],实际是电子密度ρ(x,y,z)的拓扑理论,完全将化学键数学化,即用电子密度的拓扑性质来描述化学键。
电子密度nWS是原子中特定空间位置的电子密度,即原子在Wigner-Seitz元胞界面处的电子密度,也可以称为原子Wigner-Seitz半径处的电子密度。Wigner-Seitz半径的概念是由Wigner 和Seitz 于1933年讨论金属钠的结构时提出来的[15]。而Wigner-Seitz半径处的平均电子密度概念,最早也是由Wigner 和Seitz提出的[16],最初的表达式为
中国科学家程开甲院士于1996年发表的周期表中38个元素的电子密度,实际就是对应于电子密度概念nWS的数据[6]。
需要强调的是,程开甲院士是从经典TFD方程求解出电子密度nWS,为了和Miedema的经验电子密度数据进行区别,将程开甲院士的电子密度数据称为TFDC电子密度。10多年来,我查阅了3000多篇关于(密切相关)电子密度方面的文献资料,还没有看到从经典TFD方程求解出电子密度的文献。因此,程开甲院士是第一位从经典TFD方程求解出电子密度nWS的人。
1971年,Meyer[21]等试图从经典TFD方程求解Wigner-Seitz半径处的电子密度,即nWS,但是由于边界条件选择得不正确,只得到了电子密度随半径单调增加(不正确)的图示关系,没有给出任何具体的数据,如图1所示。

表1 Miedema经验电子密度的不确定性[20, 23-25]
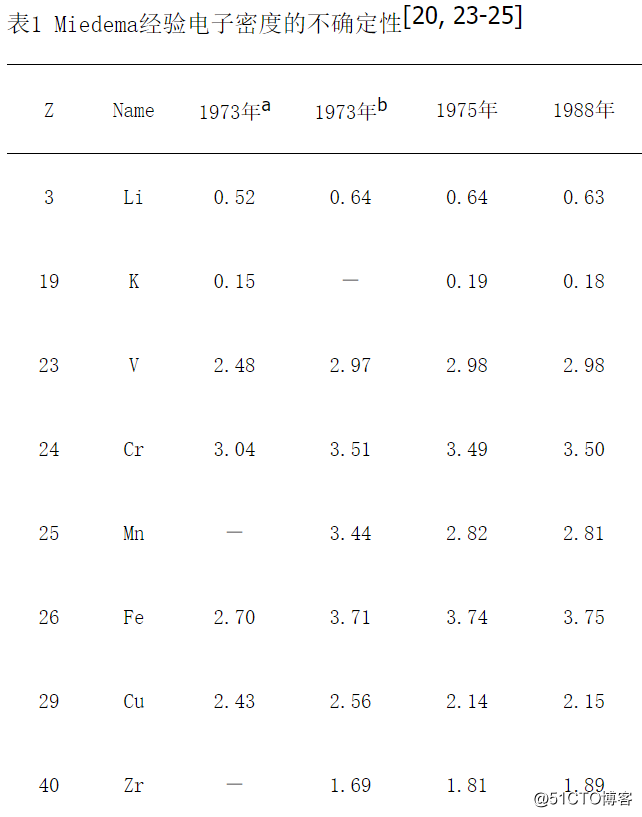

2001年,中科院金属所叶恒强院士的研究小组基于局域密度泛函的LAPW方法,计算了26个金属元素的电子密度数据[22],并且和Miedema经验公式的结果进行比较。非常遗憾的是,叶恒强院士的研究小组的文章没有提到中国科学家程开甲院士的工作,因为根据经典TFD方程求出的电子密度nWS要优于Miedema的经验计算值,因为Miedema[20, 23-25]经常毫无理由地修改自己给出的nWS数据,如表1所示。
程开甲院士从TFD方程求解出的电子密度,其精确度和准确度都非常高,因为求解TFD方程需要的惟一输入参数是Wigner-Seitz原子半径,而原子的Wigner-Seitz半径可以根据X射线衍射卡片得到。因此,程开甲院士的这种原创性的工作是对经典TFD模型的新贡献,TFDC电子密度数据可以作为元素的一个新参数而写入周期表。

此外,程开甲院士在文献[5]中,针对经典TFD模型明确提出:“原子间的边界条件只是电子密度要连续,因为这就是量子力学所要求的波函数连续的条件”。我没有考证“原子间的边界条件只是电子密度要连续”的文献背景,但是如何表述这句话却大有学问。1978年,Alonso在一篇题为Nonlocalityand the energy of alloy formation[26]的文章中,试图表述“原子间的边界条件只是电子密度要连续”,如图2所示。当原子的半径发生变化时,原子中的电子密度也必然要发生变化,即(外层)电子在原子中要重新分布,如图3所示,这种表述的正确性已经通过修正Vegard定律得到验证[31]。
② 电子密度nWS和原子组装
一般说来,电子密度ρ(x,y,z)是晶体的电子密度,可以根据密度泛函理论计算出来[27-28],也可以通过X射线衍射实验测算出来[29]。显然,ρ(x,y,z)只能表明电子在具体的晶体中的分布情况,不能描述原子组成晶体的过程。也就是说,电子密度ρ(x,y,z)只是一个具体样品的实验数据。
然而,电子密度nWS是纯元素晶体中原子Wigner-Seitz半径处的电子密度,是元素的一个参数,是确定的。实际上,电子密度nWS描述的是一种“晶格原子”[10],即把一个原子从晶体中拿出来,其电子分布仍然和在晶格环境中是一样的。晶格原子的界面处的电子密度就是nWS,如图4所示。当把原子A和原子B组装在一起时,就是图5的情形,即组成二原子AB,二原子间的平衡电子密度为nABWS。我认为,这就是未来原子组装技术的理论基础,是我10多来学习和铺垫程开甲院士TFDC模型领悟到的一个结果。

Miedema[20, 23-25]根据他的经验电子密度,建立了一个模型(被称为Miedema模型)来描述过渡元素形成合金(化合物)的生成能,公式如下:


需要强调的是,公式(6)中的参数全部都是物理量,没有人为的模型参数,在解决Vegard定律偏离实验问题(35种连续固溶体)的预言,正确率为80%[Google]。
③ TFDC电子密度的其他应用
加拿大学者Bader发表了一系列关于电子密度ρ(x,y,z)的论著,核心内容是关于电子密度ρ(x,y,z)的拓扑学分析,文献中称为Atoms in Molecules(AIM)理论[13, 32-34]。AIM理论直接对晶体(分子)的电子密度作微分,从而得到可以描述电子密度分布性质的物理量。对于电子密度作一次微分可以得到临界点的位置,比较临界点到相邻原子的距离,可以粗略地估算出两原子负电性的强弱。对电子密度的二次微分,能够得到更多临界点的数学性质。然后根据电子密度的数学性质,分析晶体(分子)的化学键特点。
需要指出的是,AIM理论的前提是要有电子密度ρ(x,y,z)的数据。
TFDC电子密度数据是元素的一种性质,通过TFDC相图[10]的计算,可以给出异类原子的平衡电子密度nABWS,这就是对应于AIM理论中临界点的电子密度。
④ TFDC电子密度和扩散溶解层
未来的原子器件是通过原子组装来制备的,可以设想,最小的原子器件是由两个原子组成的,即二原子器件。根据TFDC模型的思想,可以描述两个异类原子接触之后的平衡电子密度。相界面是由大量异类原子组成的界面,是材料科学的重要研究课题。申请者始终把TFDC模型和相界面结合起来研究:首先,通过一种实验技术让两个原来分离的相实现紧密接触;然后,通过扩散溶解反应,在接触的界面处产生一个扩散溶解层,通过分析研究产生扩散溶解层的过程,提取出异类原子接触反应的信息;最后,根据两个原子接触实现平衡的思想,来表征扩散溶解层及其形成过程。
本项目的扩散溶解层实验研究不同于Kirkendalleffect[35-38]的研究,后者主要研究原子的扩散规律和扩散偶界面标志的迁移特性。本项目研究扩散溶解层则是侧重于异类原子在接触后如何实现电子密度的平衡,同时把扩散溶解层和相图中的“横向过程”相对应,不但对未来的原子组装技术有意义,而且还启发人们从新的角度认识合金相图。
参考文献:
1.程开甲,用Fermi-Thomas方法计算金属的结合能,物理学报,14(2):16,1958
2.熊杏林,“两弹一星”功勋科学家—程开甲,北京:国防科技大学出版社,132,2003
- 程开甲,高占鹏,范启科,TF(或TFD)模型中原子的边界势及状态方程,物理学报, 33(2):176,1984
4.程开甲,程漱玉,冷压状态方程计算的新方法和材料相图研究,力学进展,21:23-30,1991
5.程开甲,程漱玉,TFD模型和余氏理论对材料设计的应用,自然科学进展,3(5):416,1993
6.Cheng Kaijia, Cheng Suyu, Theoretical Foundations of Condensed Materials, Progressin Natural Science, 6(1): 12, 1996
7.程开甲,程漱玉,基于电子理论的断裂机理新探,自然科学进展, 15(12):1528-1529, 2005
8.李世春,Zn-5Al合金超塑性的量子效应,自然科学进展,9(6): 552-557,1999
9.李世春,晶体价键理论和电子密度理论的沟通,自然科学进展,9(3):229-235,1999
10.李世春,TFDC相图,自然科学进展,13(11):1154-1159,2003
11.Debye, P. Ann. Phys.46: 809, 1915
12.Compton, A. H.,Phys. Rev. 9:49, 1917
13.Bader,R.F.W., Atoms in Molecules,Clarendon, Oxford, 1990
14.Popelier, P. L. A.,Atoms in Molecules,An Introduction, Pearson Education, 1999
15.Wigner, E. and Seitz, F.,On the constitution of metallic sodium-I, Physical Review, 43:804,1933
16.Wigner, E. and Seitz, F., On the constitution ofmetallic sodium-II, Physical Review, 46:509,1934
17.Moruzzi,V. L., Janak, J. and Williams, A.R. Calculated Electronic Properties of Metals, Pergamon,Oxford, 1978
18.Perrott,Fand Rasoltts, M, A new listing of theeffective rsvaluesfor metals, J. Phys.:Condens. Matter,6:1473-1482, 1994
19.Serebrinsky,S.A., Gervasoni, J.L., Abriata, J.P., et al., Characterizationof the electronic density of metals in terms of the bulk modulus,Journal of materials science, 33: 167–171, 1998
20.Miedema,A. R., de Boer, F.R. and de Chatel, P. F.,Empiricaldescription of the role of electronegativity in alloyformation,J.Phys. F: Metal Phys., 3: 1558,1973
21.Meyer,A.,Umar,I.H.and Yound,W.H., Lattice Spacings and Compressibilitiesvs Pauling Radii and Valencies,Phys. Rev. B4: 3287-3291, 1971
22.Cheng Dayong, WangShaoqing, and Ye Hengqiang, Calculations showing a correlation betweenelectronic density and bulk modulus in fcc and bcc metals, Phys. Review, 64B:24107, 2001
23.Miedema,A. R.,Theelectronegativity parameter for transition metals: Heat of formation and chargetransfer in alloys, Journal of the Less-Common Metals, 32:117-136, 1973
24.Miedema,A. R., ON the heat of formation of solid alloys, Journalof the Less-Common Metals, 41: 283-298,1975
25.de Boer, F.R.,et al., Cohesion in metals: transition metal alloys, New York, ElsevierScientific Pub. Co., 1988
- Alonso, J. A. and Girifalco,L. A.,Nonlocalityand the energy of alloy formation,J.Phys. F,8(12): 2455-2460,1978
27.Jansen, H. J. F. andFreeman, A. J., Structural properties and electron density of NaCl, Physicalreview, B33(12): 8629-8631, 1986
28.Robert G. Parr andWeitao Yang,Density-functional theory of atoms andmolecules,New York : OxfordUniversity Press ; Oxford [England]: Clarendon Press, 1989.
29.Coppens, P.,Hall, M.B.,Electron Distributionsand the Chemical bond, New York,Plenum Press,1982
30.James, R. C., Microscopic basis ofMiedema’s theory of alloy formation, Physical review B, 25(10): 6506-6508, 1982
31.李世春,相界扩散溶解层,东营:中国石油大学出版社,2006
32.Bader,R. F. W.,Abond path: A universal indicator of bonded interactions,J. Phys. Chem. A 102, 7314-7323,1998
33.Bader,R. F. W. and Platts,J.A., Characterization of an F-centerin an alkali halide cluster,J.Chem. Phys., 107(20): 8545-8553,1997
34.Zou,P. F., Bader,R.F. W., A topological definition of a Wigner-Seitz cell and theatomic scattering factor,ActaCryst. A50: 714-725, 1994
35.Wu,K., Morral, J. E. and Wang, Y., A phase field study of microstructuralof changes due to the Kirkendall effect in two-phase diffusion couples, ActaMaterialia, 49: 3401–3408, 2001
36.Masumura,R.A., Rath, B.B., Pande,C.S.,Analysis of Cu–Ni diffusion in a spherical geometry forexcess vacancy production,ActaMaterialia, 50: 4535–4544, 2002
37.Glund,H. L. and Gren, J. A., Analysis of the Kirkendalleffect, marker migration and pore formation, Acta Materialia, 49: 1311–1317, 2001
38.Paul, A., et. al., Bifurcation of the Kirkendall plane during interdiffusionin the intermetallic compound b-NiAl,Acta Materialia, 52: 4041–4048, 2004
TFDC电子密度
① Zn-5Al合金超塑变形后:Al相晶胞收缩,Zn相晶胞膨胀。(二原子模型)
X-射线衍射结果表明:对于再结晶态,合金中Al相的晶格收缩,点阵常数比纯Al的小,而Zn相的点阵常数大于纯Zn的。对于超塑变形态,合金中Al相的晶格收缩更为明显,而Zn相的点阵常数仍然大于纯Zn的。
为了用TFDC电子密度解释以上实验结果,我使用了一个非常简单的“二原子模型”,即只考虑两个原子,一个Al原子和一个Zn原子。我的解释是:
当Al原子和Zn原子接触时,在接触面(相界面) 应该满足量子力学波函数连续的条件,即电子密度相等。由此造成的结果是:电子密度小的原子要收缩半径,以便增大表面的电子密度;而电子密度大的原子要膨胀半径,以便减小表面的电子密度。对于晶体材料,点阵常数的变化就是原子半径的变化。因此,Zn-5Al合金中Al相晶格收缩和Zn相晶格膨胀与电子效应有关。
把以上实验结果和根据TFDC模型的解释,写成一篇题目为“Zn-5Al合金超塑性的量子效应”的论文,投给《中国科学》。论文被接受并且排了版,我也交付了中英文版面费,但是论文发排后被有关专家(能看到发排清样的专家)提出几个问题进行质疑。我根据编辑整理的质疑意见,写了非常详细的答辩意见,就是不想修改“二原子模型”,最后编辑说“争议太大”,结果文章没有被刊登。
2年之后的1999年,《自然科学进展》发表了我的这篇文章,题目仍然为“Zn-5Al合金超塑性的量子效应”(Quantum Effect of the Superplastivity inZn-5Al Alloy,用Google按题目进行学术搜索,程开甲院士引用英文版3次,中文版没有人引用)。
1999年为了申请同等学力博士学位,我在清华大学材料系为5位教授报告了我的超塑×××,也讲了“量子效应”这个实验结果和TFDC模型的解释,由于是面对面,我总算给教授们解释清楚了。后来论文评审和答辩中,有更多的专家学者看到了我的实验结果和解释。
这个实验是我自己亲自做的,使用清华大学材料系的X-射线衍射仪,重复了无数次。我的样品很特殊,具有5000%的延伸率。因此,别人的普通样品很难重复出我的结果。
1996年,我不经意地和程开甲院士提起我测量Zn-5Al合金晶格常数的事情,当告诉程开甲院士Al相和Zn相的变化趋势后,程开甲院士表现出极大的兴趣。我就是从这次讨论中领悟到了TFDC电子密度的重要性。
TFDC电子密度还有什么用呢?为此,我从价键理论和电子密度理论的关系考察了TFDC电子密度。
② 原子作用体积
TFDC电子密度的量纲是单位体积内的电子数,由于单位体积内的电子数目很大,一般表示为1023/m3。
需要强调的是,这是在原子Wigner-Seitz半径处的电子密度值。Wigner-Seitz半径处就是原子和原子接触的界面,是原子和原子的外层电子相互作用的地方,也是这种相互作用使原子实现化学键结合,形成晶体(或者别的什么状态)。如果能估算出原子外层电子的作用范围,即外层电子作用的空间范围,我把这个空间范围称为原子作用体积。那么,原子作用体积乘以TFDC电子密度应该等于参与成键外层电子数目,即价键电子数。
一边是TFDC电子密度,另一边是价键电子数,能把它们联系起来需要一个“体积”因子作为桥梁。为此,我把这个体积因子定义为“原子作用体积”:
原子作用体积等于Wigner-Seitz原子与密堆积原子的体积差。换句话说就是,用Wigner-Seitz原子半径计算出的原子体积要比用刚球密堆积原子半径计算的原子体积大,它们的差就是原子作用体积。
对元素周期表绝大多数固体元素计算表明,TFDC电子密度乘以原子作用体积,就等于价键电子数,与Pauling和余瑞璜给出的值基本相符。
1999年,我把原子作用体积的概念和计算结果写成论文发表在《自然科学进展》,题目为“晶体价键理论和电子密度理论的沟通”(Relationshipbetween the valence electron theory and the electron density theory in crystal,用Google按题目进行学术搜索,中文版被别人引用2次,用了我的原子作用体积公式,计算了他们自己的实验结果,英文版没有搜索到)
这是使用Pauling和余瑞璜的价键电子数证明了TFDC电子密度概念的意义。此外,我通过修正Vegard定律,再一次用实验数据证明了TFDC电子密度的重要性。
③ TFDC相图(atomic phase diagram,原子相图)
Vegard定律在多数情况下偏离实验结果,也就是说,Vegard定律在多数情况下并不成立,但是Vegard定律被写进了各种教科书,可能是惟一的在多数情况下不成立的而且被广泛接受的定律。
发表了“原子作用体积”之后,我就开始思考用TFDC电子密度来修正Vegard定律,2002年有了定性的结果,2003年有了定量的结果。这个工作给我带来一个副产品—TFDC相图。2003年,我在《自然科学进展》先发表了“TFDC相图”,2006年才把根据TFDC相图修正Vegard定律的内容写到《相界扩散溶解层》,因为前者比后者要重要。(这篇文章的英文名称为atomic phase diagram,用Google按题目进行学术搜索,还没有人引用)。
我用TFDC相图考察了35个连续固溶体合金,只有7个合金系和实验数据不符。需要指出的是,我的理论非常简单,只用到组元的原子半径、TFDC电子密度和组元晶体的结合能三个物理量,没有任何人为的模型参数。
以上三件事情以及我自己的研究方向“从超塑性到TFDC模型的过渡”,在《相界扩散溶解层》里都有非常详细的叙述。
现在问题已经明确:TFDC电子密度是程开甲院士的源头创新(3000篇文献检索结果),程先生自1958年发表第一篇关于TFD模型的研究论文,25年的×××研究和试验工作也用到了TFD模型,2005年还第一作者发表研究论文(自然科学进展,12期)。2006年10月,我和程开甲院士讨论了一个下午的TFDC模型,我对程先生说,TFDC电子密度可以用来建立一种原子组装理论。程先生胸有成竹地点点头,因为我和程先生第一次见面是在“材料设计研究” 面上基金集团管理项目研讨会上,而原子组装应该是材料设计的最高境界。此外,程先生在论文中明确写道:“改进的TFD模型可以作为固态物理理论研究的一个‘探针’,为实际材料设计提供了方法和手段”。探针的灵敏度极限是探测一个或者几个原子,而原子组装理论就需要这样的探针。
我刚才讲述的那三件事情,实际上都是在原子层次上做文章:“二原子模型”投稿于1996年,发表于1999年;“原子作用体积”发表于1999年;“原子相图”发表于2003年。
围绕TFDC的工作,尽管时间跨度10多年,但是却前呼后应,相当默契。然而,这一切都是由TFDC电子密度导演的,下一个要出场的角色是最令人遐想的概念—原子组装。
人们先把沙土制成秦砖汉瓦,然后用砖瓦来盖房子。同样的道理,先把元素周期表中的两个或者几个异类原子组装成原子砖,根据TFDC电子密度定义原子砖的参数;然后用原子砖来“组装”纳米材料或者原子器件,再使用一定的模型计算出纳米材料或者原子器件的技术参数,这就是我根据TFDC电子密度领悟到的原子组装理论。例如,只考察Ni和Ti两个原子,就可以估算Ni原子和Ti原子组成的化合物或固溶体的某些参数。
转载自原文链接, 如需删除请联系管理员。
原文链接:程开甲院士和他的TFDC模型,转载请注明来源!
