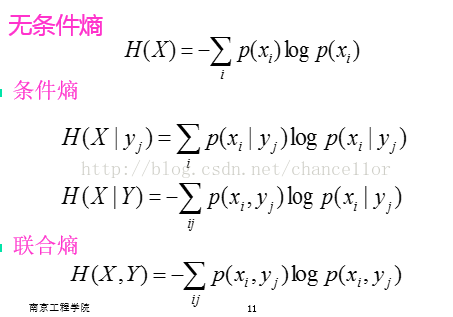第三章数据压缩的基本技术 -一个渣渣

第三章数据压缩的基本技术

1、数据压缩的理论基础：香农的信息论

2、压缩方法的分类？

无损：无失真的100%的复原，压缩比相对来说不高

数据无损压缩的方法：霍夫曼编码(Huffman coding )、算术编码(arithmetic coding)、行程长度编码(run-lengthcoding)、词典编码(dictionary coding)

有损：到达接收端时有损失，无法100%的复原

3、信源相关的参数？ P29

信息量(informationcontent)：具有确定概率事件的信息的定量度量

在数学上定义为

其中是事件出现的概率

举例：假设X={a,b,c}是由3个事件构成的集合，p(a)=0.5，p(b)=0.25，p(b)=0.25分别是事件a, b和c出现的概率，这些事件的信息量分别为，

I(a)=log2(1/0.50)=1 sh

I(b)=log2(1/0.25)=2 sh

I(c)=log2(1/0.25)=2 sh

一个等概率事件的集合，每个事件的信息量等于该集合的决策量。

熵(entropy)：按照香农(Shannon)的理论，在有限的互斥和联合穷举事件的集合中，熵为事件的信息量的平均值，也称事件的平均信息量(mean information content)

用数学表示为

-------------------------------------------------------------------------

联合熵？条件熵？互信息？

------------------------------------------------------------------------

4、数据压缩的具体方法？

预测编码（概念）P37、正交变换编码（概念）、子带编码、小波变换编码（概念）、熵编码

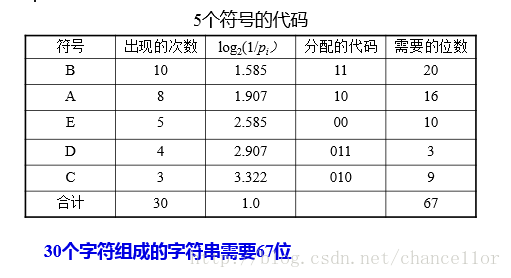
熵编码：基于统计的原理编码，不定长编码（大概率用短码，小概率用长码），费诺和哈夫曼编码。

预测编码：实际上是利用了信号之间的关联性，用前面出现的信号去预测当前的信号，对他们的差值进行编码，有两种编码方法是差分脉冲编码调制（DPCM）和自适应差值脉冲编码调制ADPCM

变换编码：

对于有记忆信源，由于信源前后符号之间具有较强相关性，要提高信息传输的效率需解除信源符号之间的相关性，解除相关性可在时域上进行（如前面介绍的预测编码方法），也可以在变换域上进行，即变换编码方法。

变换编码是指在发送端，先对信号进行映射变换，然后再针对变换后的信号进行量化和编码；在接受端，则先将收到的信号进行解码等操作，然后再进行反映射变换，以再现原始信号。

子带编码：利用信号在频域中分成若干段，在每一段中单独进行量化和编码，把噪声抑制在每一段中，因此弱信号就有可能被我们检测出来，不会被漏掉。在每一个频域里可以用自己的技术。

小波变换：小波偶函数和小波奇函数进行一个比较，它在一个时移时间函数和伸缩因子上面进行变换。

*简答预测编码和变换编码的概念？

*DPCM和ADPCM之间的区别？

它与脉冲编码调制(PCM)不同的是，PCM是直接对采样信号进行量化编码，而DPCM是对实际信号值与预测值之差进行量化编码，存储或者传送的是差值而不是幅度绝对值，这就降低了传送或存储的数据量，可适应大范围变化的输入信号。为了进一步提高编码的性能，将自适应量化技术和自适应预测技术结合在一起用于差分脉冲编码调制DPCM中，从而实现了自适应差分脉冲编码调制ADPCM。

------------------------------------------------------------------------------------------

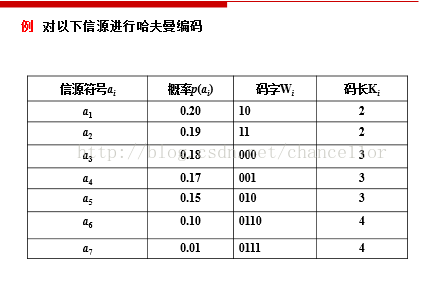
*哈夫曼编码会编码！？码字是从右到左来写！平均码长=（码长*概率）加权求和！