这几天需要用OpenGL做一个小程序,之前没有计算机图形学和OpenGL的基础,以为很简单(事实上确实不难),但是在自己摸索的过程中却走了一些弯路。现在稍微总结一下。
1 坐标系统
从定义一个零件的几何外形到图形设备上生成相应的图形,需要建立相应的坐标系统来描述,并通过坐标变换来实现图形的表达。有几个坐标系需要了解一下。
1. 1 世界坐标系(world coordinate system)
或者把它叫做场景坐标系吧,是一个三维坐标系,多用右手直角坐标系,用来描述物体所处的场景空间。坐标原点在屏幕中心,Z轴垂直于屏幕指向屏幕外,y轴竖直向上,x轴水平向右。
1.2 物体本地坐标
用来定义某个实体本身的坐标系。例如,stl文件中包含了构成实体模型的三角面片的顶点坐标,这里的顶点坐标值就是在物体本地坐标系下的坐标值。
1.3 设备坐标系(device coordinate system)
也称为物理坐标系,是一个二维坐标系,与图形输出设备相关联,用来表示三维模型投影后生成的二维图形显示在图形输出器(例如显示器)的坐标系。单位是象素(对于显示器来说)。
1.4 规格化设备坐标系(normalized device coordinate system)
这是一个人为规定的假象设备坐标系,与设备无关,目的是为了方便将图形软件应用到不同分辨率的设备。该坐标系的坐标轴方向以及原点与设备坐标系相同,但是它最大的坐标范围是1.
首先将输出图形转换为规格化设备坐标系,当转换到具体的不同输出设备时,只需要将图形的规格化坐标系再乘以相应设备分辨率即可,这样使图形软件与图形设备分离开来,增加了图形软件的可移植性。
2 投影(projection)和视景体(viewing volume)
我们在3D坐标系统定义模型,但是我们在屏幕上显示模型时只能使用二维坐标系,从三维坐标转换到二维坐标,这里就需要用到投影。我们可以用正投影(orthographic projection)或者透视投影(perspective projection)。关于这两个投影的性质就不讲了,网上很多。
2.1 视景体
我个人觉得这是很重要的一个概念,简单地来说,视景体就是三维空间中的一个封闭区域。在这个区域内的模型才能被显示在屏幕上,在这个区域外的部分会被裁剪掉,不会显示在屏幕上。视景体的大小范围是可以设置的,具体方法就是用上面的两种投影。
2.2 通过正投影设置的视景体
正投影设置的视景体是一个长方体,我们通过设置视景体xyz轴最大最小坐标来定义它。在OpenGL中可以用
GLFrustum::SetOrthographic(GLfloat xMin,GLfloat xMax,GLfloat yMin,GLfloat yMax,GLfloat zMin,GLfloat zMax)来定义,也可以用glOrtho(left, right, bottom, top, near, far)来定义。
在正投影中,观察者的位置假定在z轴正无穷处。

图片来源于网络,原网址是http://jerome.jouvie.free.fr/opengl-tutorials/Lesson1.php#ClippingPlane
2.3 通过透视投影设置的视景体
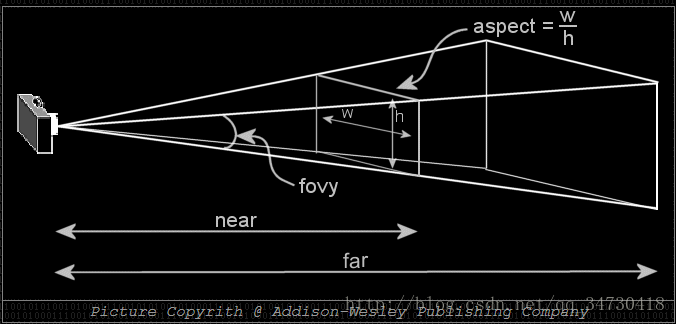
透视投影设置的视景体是一个平截头体(frustum),它的形状是一个金字塔被截去塔尖之后的形状。
图片来源于网络,原网址是http://jerome.jouvie.free.fr/opengl-tutorials/Lesson1.php#ClippingPlane
在OpenGL中我们可以用GLFrustum::setPerspective(float fFov,float fAspect, float fNear,float fFar)或者gluPerspective(fovy, aspect, near, far)来定义。
在透视投影中,观察者的位置默认在坐标原点(0,0,0),从z轴正向看向z轴负向。为了我们的模型落在视景体内,我们还需要经过一些变换。
3 变换
3.1 点的齐次坐标表示
齐次坐标是将一个n维空间的点用n+1维的向量来表示,即附加了一个坐标。也就是说,我们使用一个四维行向量(或者说1X4的矩阵)[x,y,z,w]来表示三维空间中的一个点(x,y,z)。采用齐次坐标系的优点:(1)为几何图形的二维、三维甚至更高维空间的坐标变换提供统一的矩阵运算方法。(2)处理无穷远点比较方便。
3.2 图形变换
变换矩阵
为了将一个模型放到一个场景中,摆在某一个位置,朝着某个方向,这就要将模型在本地坐标系下的值转换到场景坐标系下的值,我们用矩阵运算来实现这一点。一个变换矩阵表示了场景空间中的一个特定位置,以及相对于视觉坐标系的3个轴上的方向。
一个4X4变换矩阵的第一个列向量表示本地坐标系x轴在场景坐标系中的方向,第二个列向量表示本地坐标系y轴在场景坐标系中的方向,第三个表示z轴在场景坐标系中的方向,第四列表示本地坐标系的原点在场景坐标系下的位置。也就是说,通过变换矩阵运算,我们把本地坐标系的原点放在了场景坐标系中的一个点,把本地坐标系的xyz轴对准了某个方向,这样就在场景中摆放好了我们的模型。
拿二维举例来说:

上面这个矩阵将物体坐标系原点放到场景坐标系的(2,2)处,物体坐标系的x轴朝着(1,0)方向,y轴朝着(0,-1)方向。物体本地坐标系下的(1,1)点在场景坐标系下的坐标点为(3,1),画个坐标图的话一目了然。
转载自原文链接, 如需删除请联系管理员。
原文链接:计算机图形学入门,转载请注明来源!