TCA（Transfer Componet Analysis）是一种边缘分布自适应方法，属于迁移学习中数据分布自适应的一种经典方法。由香港科技大学Q Yang教授及其团队于2011年提出。下面对相关问题和方法进行总结。

问题描述

在我们构建机器学习模型时，训练数据Xs的分布P（Xs）于 测试数据（或者是实际应用数据）Xt的分布P（Xt）并不一致。这会导致我们训练出的模型的鲁棒性变差，并且在测试中可能很难有一个好结果。在本文中，我们将Xs所在的数据域称为源域（surce domain）Xt所在的数据域称为目标域（target domain）。

解决办法

maximum mean discrepancy:

为了解决这个问题，我们想要学习一种映射，使

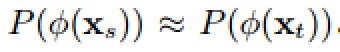
这样二者的条件分布也会近似

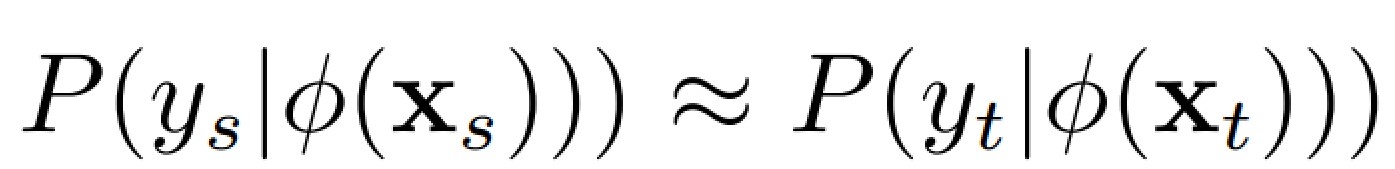
这里就有一个问题，如何衡量两个域的分布的距离？只有有可量化的距离我们才能衡量并且构造函数使源域和目标域在某个映射下距离最小。
在TCA中用到了**最大均值差异 (MMD， maximum mean discrepancy) **。设n1、n2为两个域的实例个数 ：

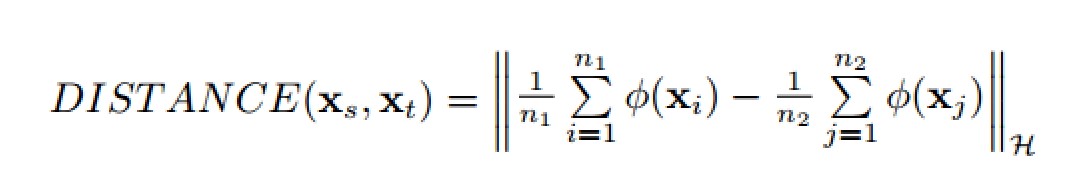
MMD，最先提出的时候用于双样本的检测（two-sample test）问题，用于判断两个分布p和q是否相同。它的基本假设是：如果对于所有以分布生成的样本空间为输入的函数f，如果两个分布生成的足够多的样本在f上的对应的像的均值都相等，那么那么可以认为这两个分布是同一个分布。现在一般用于度量两个分布之间的相似性。[1]
通过这种方式就可以衡量连个数据域之间的距离。我们构造的函数只需要是的上面式子最小就可以了。
###核的学习
有了距离的量化，我们就可以试图去寻找我们需要的映射了。但是这里有一个问题，我们想要构造的函数会非常复杂，是一个高维的极其复杂的函数，如果数据很大的情况这种函数需要极大的运算量，甚至难以构造，这个高阶非线性的函数。直接求解非常困难，属于SDP问题。通过文章Sinno Jialin Pan, James T. Kwok, and Qiang Yang. Transfer learning via dimensionality reduction. In Proceedings of AAAI, pages 677–682, Chicago, Illinois, USA, 2008. 把这个问题转化成了一个核函数学习的问题。
核函数：

通过把这个函数的求解问题改成核函数的求解问题，大大的减小了运算量。

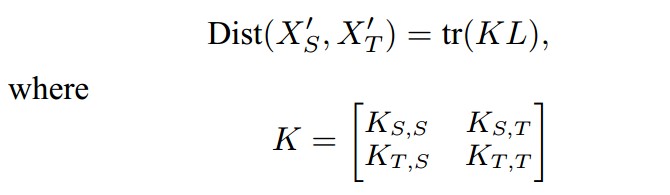
在这基础上，Q Yang教授团队又进一步的做了推导：
将K矩阵分解为

利用W将上述矩阵分解为：


到了这里，我们的距离公式就可以变成：


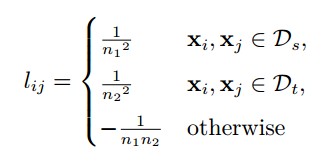
整理一下可以得到:

上面基本介绍了TCA的整个推导过程，借用 中国科学院计算技术研究所 王晋东博士在《迁移学习简明手册》中的话总结一下要用TCA方法到底需要怎么计算。
输入是两个特征矩阵，我们首先计算 L和 H 矩阵，然后选择一些常用的核函数进行映射 (比如线性核、高斯核) 计算 K，接着求

的前 m 个特征值。仅此而已。然后，得到的就是源域和目标域的降维后的数据，我们就可以在上面用传统机器学习方法了。
#实现代码
中国科学院计算技术研究所王晋东博士在GitHub上有一套开源的TCA代码，在这里贴在下面方便大家学习。
https://github.com/jindongwang/transferlearning/tree/master/code/traditional/TCA

#文中内容部分摘自中国科学院计算技术研究所 王晋东博士在《迁移学习简明手册》和香港科技大学Q Yang教授2011年的论文：Domain Adaptation via Transfer Component Analysis

[1]xiaocong1990: https://blog.csdn.net/xiaocong1990/article/details/72051375

转载自原文链接, 如需删除请联系管理员。

原文链接：【迁移学习】TCA小结，转载请注明来源！