来源 | 睿慕课

机器人动力学研究最基础的是建立完整的动力学方程,这其中最关键的是建立多连杆机构的动力学方程。笔者以经典的PUMA560机器人构型为例,阐述四种不同的机器人动力学形式及函数文件。计算环境为matlab,方便研究者的使用。
1 拉格郎日形式
这是基于拉格朗日方程所建立的动力学表达式,其形式如下:

其中各项的求取过程如下:

基于如上推导过程,笔者写了如下的函数
LagrangeRobot(DH参数,杆件质量,杆件质心,杆件惯性张量)
2 牛顿-欧拉形式
基于牛顿-欧拉方程建立,出于第三种形式的考虑,这里要分别建立基于机器人标准DH模型与修改DH模型的动力学方程。以标准DH模型为例,它的主要推导过程如下:

基于如上推导过程,笔者写了如下的函数:
NewtonEulerSDHRobot(DH参数,杆件质量,杆件质心,杆件惯性张量)
小结:形式二的计算效率远高于形式一,经统计,形式一得进十分钟,形式二一分钟左右;但形式一的方程形式明确,具有很强的物理意义,对于控制推导来说意义重大。
3 参数(线性)分离形式
首先要基于修改DH模型与牛顿-欧拉方程求取机器人动力学方程;再通过如下的迭代递推方程:

最终获取如下参数分离的线性化动力学表达式:

这里的p是由各连杆的惯性参数组成的(每根杆件10个),它与关节的位置、速度、加速度等状态变量均无关。
基于如上推导过程,笔者写了如下的函数:
LinearizedRobot(DH参数,杆件质量,杆件质心,杆件惯性张量)
4 最小惯性参数形式
首先要基于修改DH模型与牛顿-欧拉方程求取机器人动力学方程;再通过如下的迭代递推方程:

形式四是由形式三进一步化简获得的。形式三有一个重大缺陷:Y矩阵列不满秩,它有些列为0,有些列间线性相关。这对于参数辨识及一些自适应控制是极为不利的,需做如下处理 ,其中
 列满秩。具体推导过程可参考如下提问。
列满秩。具体推导过程可参考如下提问。
问:如何讲串联机器人动力学方程化成线性形式?
串联结构的动力学一般式是这样的吧,当然,我用matlab迭代过,6自由度的解析式是超过10万个字符,matlab 都显示不完,所以也没法写成t1=。。。。t2=。。。类似这种解析解。

然而,动力学参数很难确定,什么质量什么的,实测出的数据根本用不了,误差贼打,只能参考论文的线性化方法,但是这个看不懂:

请教是如何把一般式转化成线性式,把theta变成一个无关角度,速度,加速度的函数,到底是这么求出来的。。。。。这个转化方法是基于一种什么方法呢。。。。。谢答!
这是我在复现机器人经典运动学理论、动力学理论及控制理论中遇到最困难的一环,我也是最近才把这个问题解决掉,这里先简单分析下过程,以后会再整理下。
1.通过标准DH参数与变形的牛顿-欧拉迭代,可获得如下形式的动力学方程
 。
。
2.由于Q中有列为0或列与列间存在线性关系;借由最小惯性参数理论(minimum inertial parameters 或 base inertial parameters),将参数p化为 。
3.最终即可获得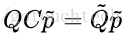
 是列满秩的。
是列满秩的。
转载自原文链接, 如需删除请联系管理员。
原文链接:机器人动力学方程的四种形式,转载请注明来源!
