转自:http://blog.sina.com.cn/s/blog_620bf89501011g60.html
在三维空间中,选择一个点,记该点为投影中心,不经过这个点再定义一个平面,称该平面为投影面,从投影中心向投影面引出任意条射线,称这些射线为投影线;穿过物体的投影线将与投影面相交,在投影面上形成物体的像,称这个像为三维物体在二维投影面上的投影。这样将三维空间的物体变换到二维平面上的过程称为投影变换。
投影分类:
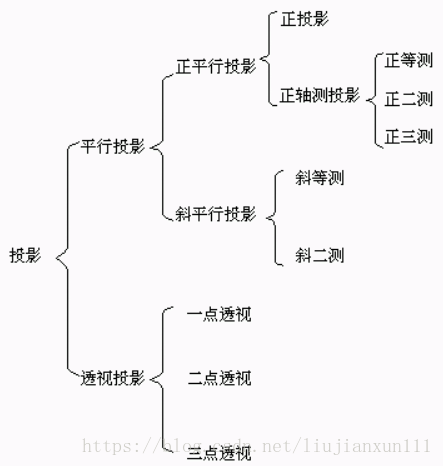
投影变换:
分为透视投影和平行投影,其主要区别在于透视投影的投影中心到投影面之间的距离是有限的,而平行投影的投影中心到投影面之间的距离是无限的。当投影中心在无穷远时,投影线互相平行,所以,平行投影表示时只给出投影线方向即可,而透视投影要明确指定投影中心的位置。
平行投影:
平行投影根据投影方向与投影面的夹角分为两类,即正平行投影与斜平行投影,当投影方向垂直于投影面时称为正平行投影,否则为斜平行投影。
正平行投影(三视图):
正平行投影的投影中心到投影面之间的距离是无限的正投影。正平行投影又包括:三视图和正轴测。
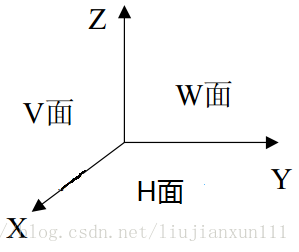
三视图:
工程中通常将三维坐标系 OXYZ 三个坐标平面分为:H 面(XOY 面)、V 面(XOZ 面)和 W 面(YOZ 面)。三维图形在 V 面上的投影称为主视图、在 H 面上的投影称为俯视图、在 W 面上的投影称为侧视图。
主视图:
将三维形体向 xoz 面(又称 V 面)作垂直投影(即正平行投影)得到主视图。
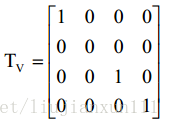
俯视图:
三维形体向 xoy 面(又称 H 面)作垂直投影得到俯视图。
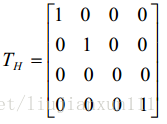
侧视图:
获得侧视图是将三维形体往 yoz 面(侧面 W)作垂直投影。
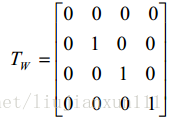
正轴侧投影变换:
若将空间立体绕某个投影面所包含的两个轴向旋转,再向该投影面作正投影,即可得到立体正轴测图。通常选 V 面为轴侧投影面,所以将立体图绕 Z 轴正向(逆时针方向)旋转θ角,再绕 X 轴反向(顺时针方向)旋转φ角,最后向 V 面正投影。因此将绕 Z 轴旋转变换矩阵 Tz,绕 X 轴旋转变换矩阵 Tx 和向 V 面正投影变换矩阵 Tv 连乘,即可得到正轴侧变换矩阵:
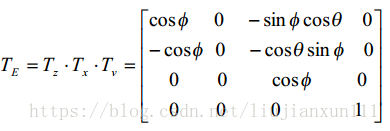
正等侧投影:
正轴侧投影中 x、y、z 三个方向上缩放率相等时的变换,即 θ 为 45度,φ 为 35 度 16 分,变换矩阵为:

正二侧投影:
正轴侧投影中 x、y、z 两个方向上缩放率相等时的变换,即 θ 为 20 度 42 分,φ 为 19 度 28 分,变换矩阵为:

斜平行投影:
假设 Z=0 的坐标平面为观察平面(H 面),点(x,y)为点(x,y,z)在观察平面上的正平行投影坐标,点(x/,y/)为斜投影坐标。(x,y)与(x/,y/)的距离为 L。
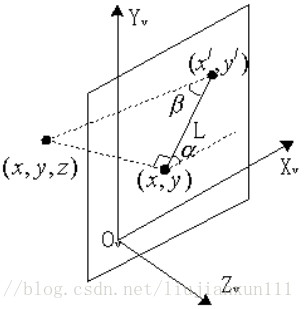
可得斜平行投影的变换矩阵:
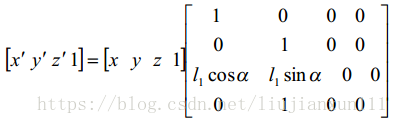
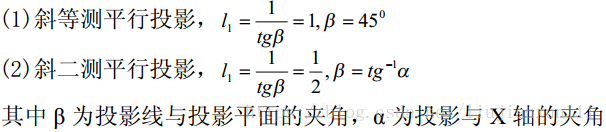
透视投影:
透视投影的视线(投影线)是从视点(观察点)出发,视线是不平行的。不平行于投影平面的视线汇聚的一点称为灭点,在坐标轴上的灭点叫做主灭点。主灭点数和投影平面切割坐标轴的数量相对应。按照主灭点的个数,透视投影可分为一点透视、二点透视和三点透视。
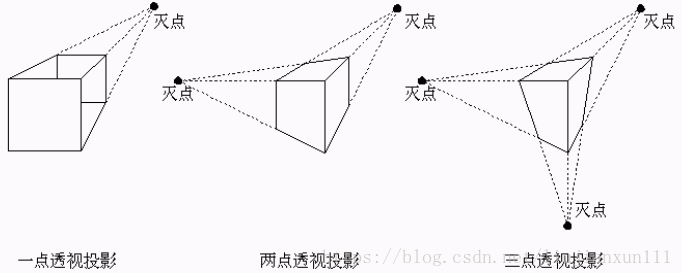
一点透视:
Z 轴上有一个观察点 V(0,0,h),由 V 点出发将物体的点 P(x,y,z)投影到 XOY 平面上得到(X,Y,Z)。
灭点在 Z 轴上(0,0,-h):
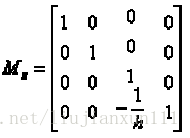
灭点在 X 轴上(-h,0,0):
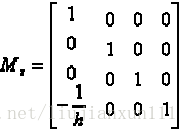
灭点在 Y 轴上(0,-h,0):
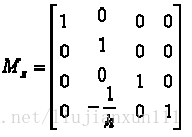
二点透视:
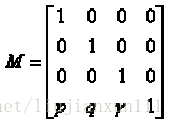
若 p,q 二个参数不为零,则即可得到二点透视

三点透视:

透视投影技巧:实际进行透视投影时,为了获得理想的透视投影图,往往先对物体进行旋转和平易,然后再进行透视投影变换。
转载自原文链接, 如需删除请联系管理员。
原文链接:三维投影变换,转载请注明来源!
